Sublinear Curved Edge Detection

Curved Edge Detection in Sublinear Time
Oct. 2016

Introduction
Problem Setup
A Sublinear Approach to Curved Edge Detection
Results
Code
References

1. Introduction

Edge detection is fundamental to image analysis and many algorithms have been developed for this task over the past few decades. In this work we assume the classical model of piecewise constant images and focus on detecting edges with step discontinuity. One of the most widely used algorithms for detecting step edges is [3] , which runs in linear time in the image size. The more recent Line Segment Detector (LSD) [4] , aimed specifically at detecting straight edges, has similar runtime complexity. In addition, both methods were designed to perform well only at low noise levels.

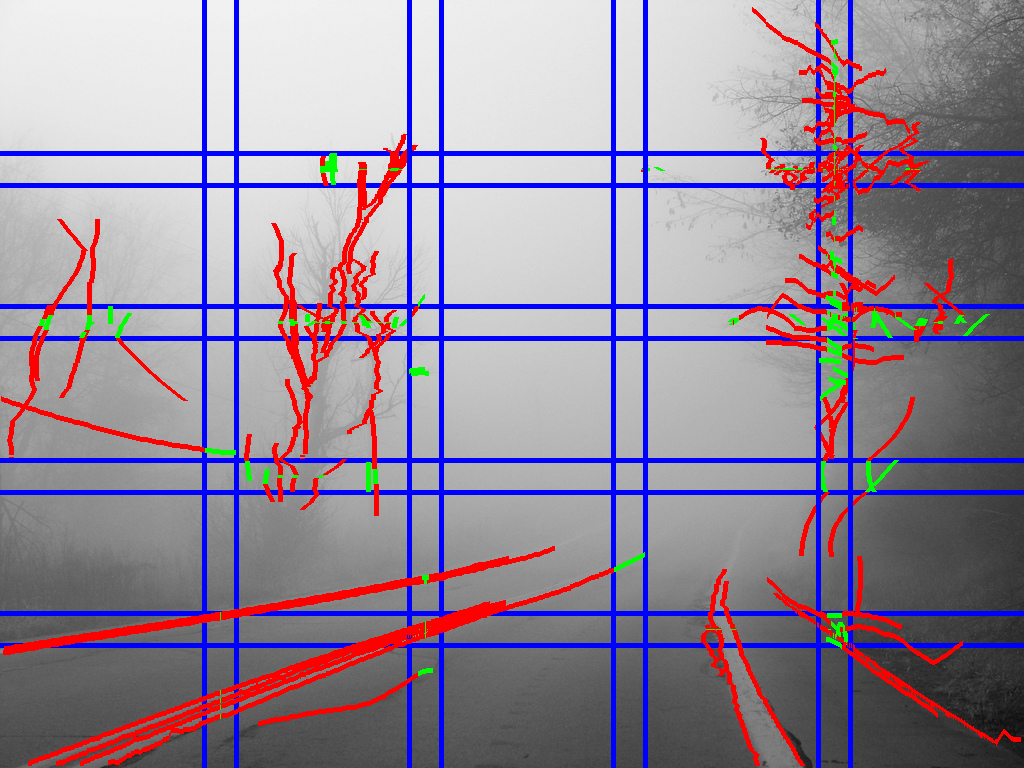
Various practical applications, however, require edge detection under very restrictive conditions. For instance, cameras mounted on cars or drones for avoiding crashes should be able to detect lanes or power lines under poor visibility conditions, such as the extreme fog shown in Fig. 1. Furthermore, images are typically acquired and stored by hardware, such as a CCD camera, and the requirement of processing them in real time may limit their transfer from memory to CPU and subsequent analysis to only a fraction of all image pixels. This motivates the following question:

How well can one detect edges in noisy images under severe computational constraints?

The problem was partially treated in [2] where the authors focused on detecting long and straight step edges. Their key idea was that, to detect long edges, it is not necessary to process all image pixels, but rather only a small subset. We extend their work and present a novel algorithm for detecting long and possibly curved edges, again with runtime sublinear in the total number of image pixels.

2. Problem Setup

Let $I_c(x,y)$ be a noise-free function defined on a rectangular domain $\Omega \subset \mathbb{R}^2$ . As a simple image formation model, let $I$ be the discrete image of size $n_x \times n_y$ pixels, obtained by ideal sampling of $I_c$ (with a $\delta$ point spread function) on a uniform rectangular grid, and corrupted by additive noise

I_{i, j} = I_{c} (h_{x} \cdot i, h_{y} \cdot j) + ξ_{i, j} .

$\begin{equation} I_{i,j} = I_c(h_x \cdot i, h_y \cdot j) + \xi_{i,j}. \end{equation}$

For simplicity, we assume that the noise is i.i.d. Gaussian, $\xi_{i,j} \sim N(0,\sigma^2)$ with known variance $\sigma^2$ , and independent of $I_c$ . When $\sigma$ is unknown, it can be estimated from the image (see [6] ,[7] for a review of noise estimation methods). Finally, in what follows, for notational clarity we consider square images with $n_x = n_y = n$ .

The key question is detecting possibly curved edges with sublinear time complexity. We study this problem under the following simplified image model: the noise-free function $I_c$ is piecewise constant, with constant values in different regions $\Omega_i\subset \Omega$ . The boundaries between adjacent regions $\Omega_i$ delineate long and potentially curved edges $\Gamma_i$ . Note that we make no assumptions on the sizes or shapes of the regions $\Omega_i$ . Fig. 2 shows such an image with 3 regions.

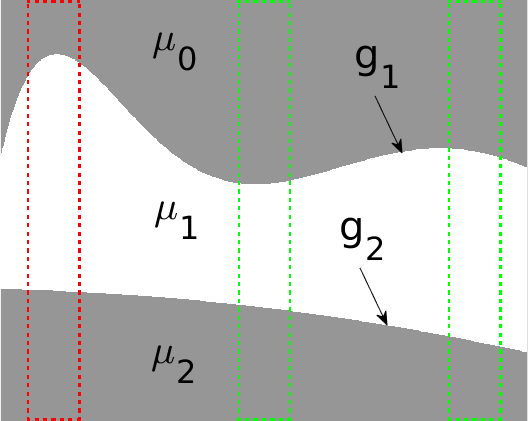
3. A Sublinear Approach to Curved Edge Detection

Given the noisy image $I$ , our goal is to detect and localize the long and smooth edges in it, with a time complexity sublinear in the image size. In particular, analogous to [2], our algorithm initially samples only $O(n^\beta)$ of all image pixels for some $\beta < 2$ . Specifically, we detect edges in a few strips extracted from the input image.

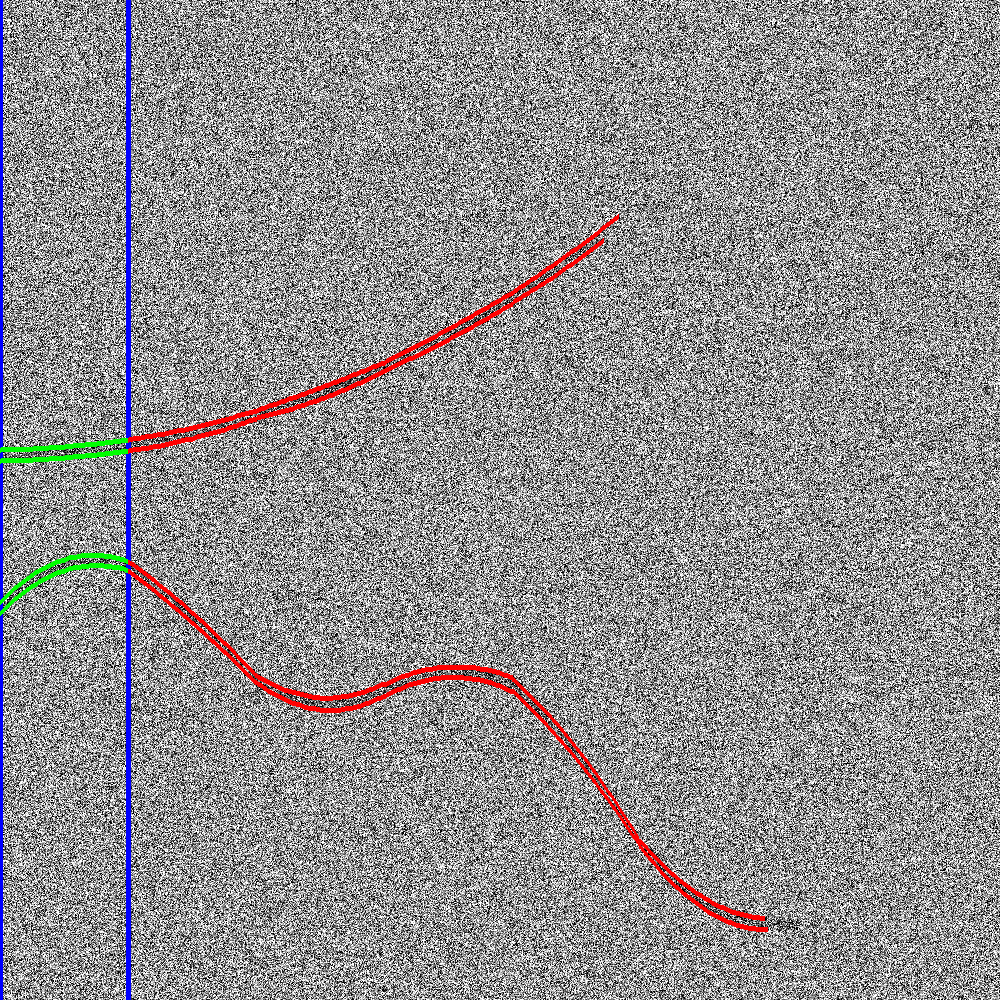
Since we aim to detect general-shaped smooth edges, matching detected edges in adjacent strips, as done in [2], is no longer a viable strategy. Instead, we propose to track the detected edges outside the strips (see Fig. 3 for an illustration). Here we only outline the algorithm. For more details on advanced issues such as non-maximal suppression and improved edge localization, see sections 5.4 of [1].

Input

$I$ - an $n \times n$ noisy image
$\sigma$ - noise level
$L$ - width of each strip
$w$ - half width of mask
$\alpha_d,\alpha_t$ - false detection rates

Output

A list of detected edges

Algorithm:

Extract several detection strips of width $L$ from the noisy image.
Detect edges within each strip (using detection false alarm rate $\alpha_d$ )
Track the detected edges (using tracking false alarm rate $\alpha_t$ )

4. Results

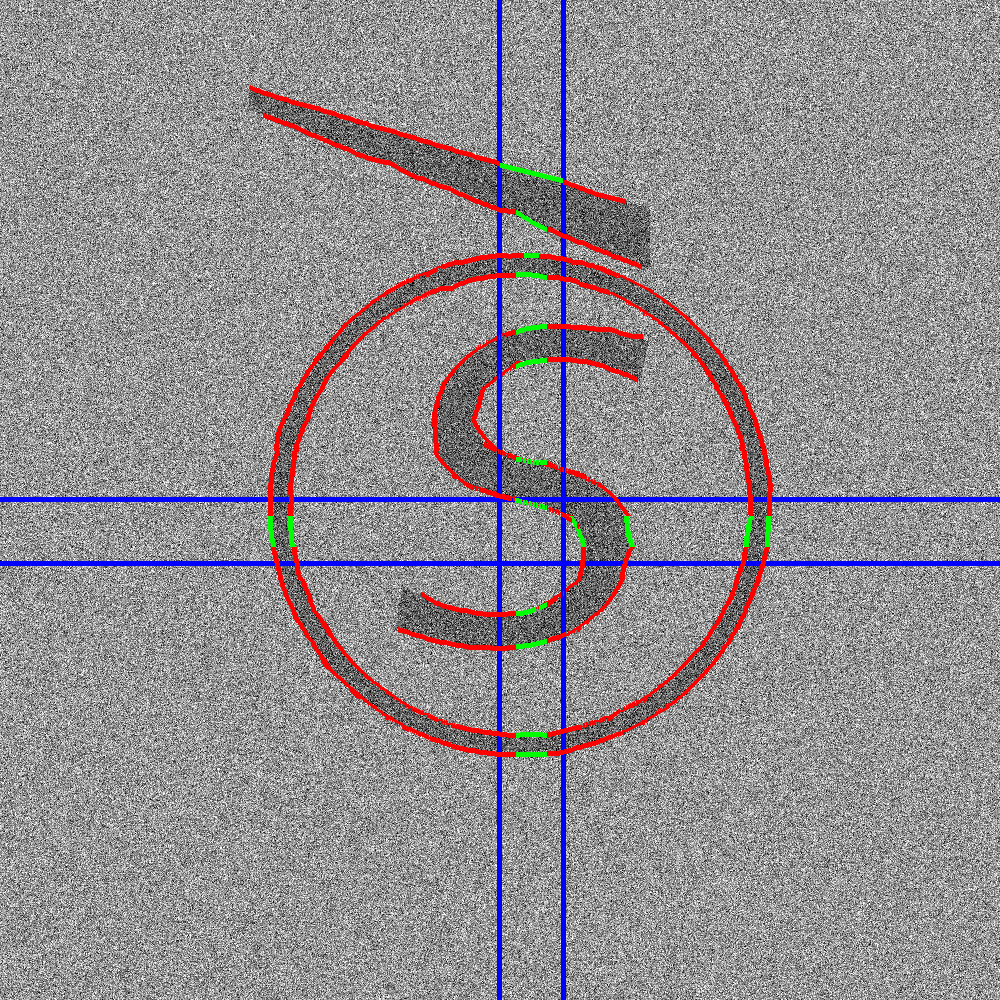
We first compared our algorithm to the Canny Edge Detector [3] and the Line Segment Detector (LSD) [4] (implementation available at [5]) on a $1000 \times 1000$ synthetic image (see Fig. 4). Noise was added to generate two test cases with SNR equal to 2 (top row) and 1 (bottom row) respectively. The results show that our algorithm (3rd column) was less prone to false alarm than Canny (5th column) and was more robust, compared to LSD (4th column), for detecting particularly curved edges.

Fig. 4 - Curved edge detection under different SNRs. Here two strips (one horizontal and one vertical) were extracted from the inputs for detecting edges.

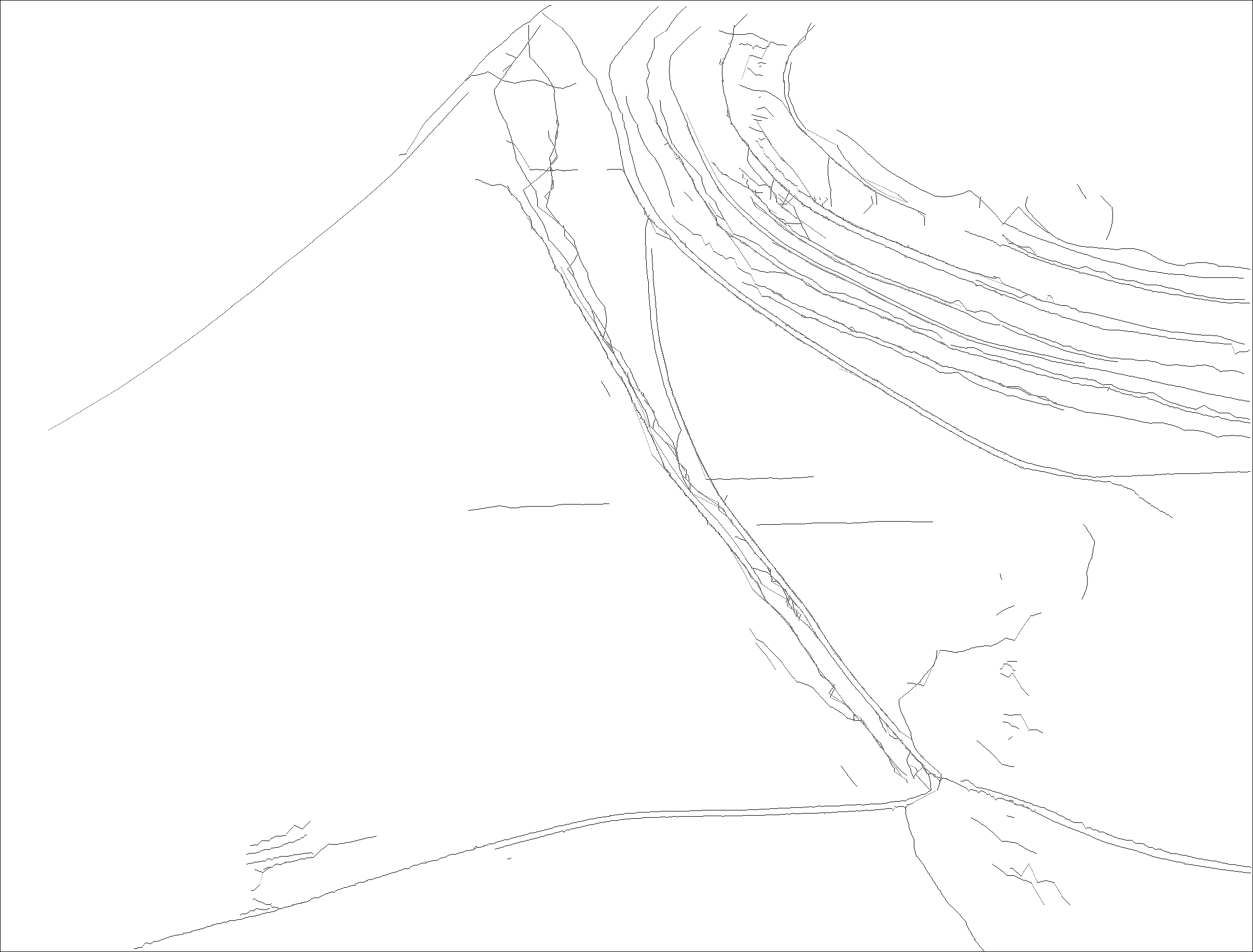
Next, we show some results on natural images. For details on the parameters used to produce these results, see section 6 of [1].

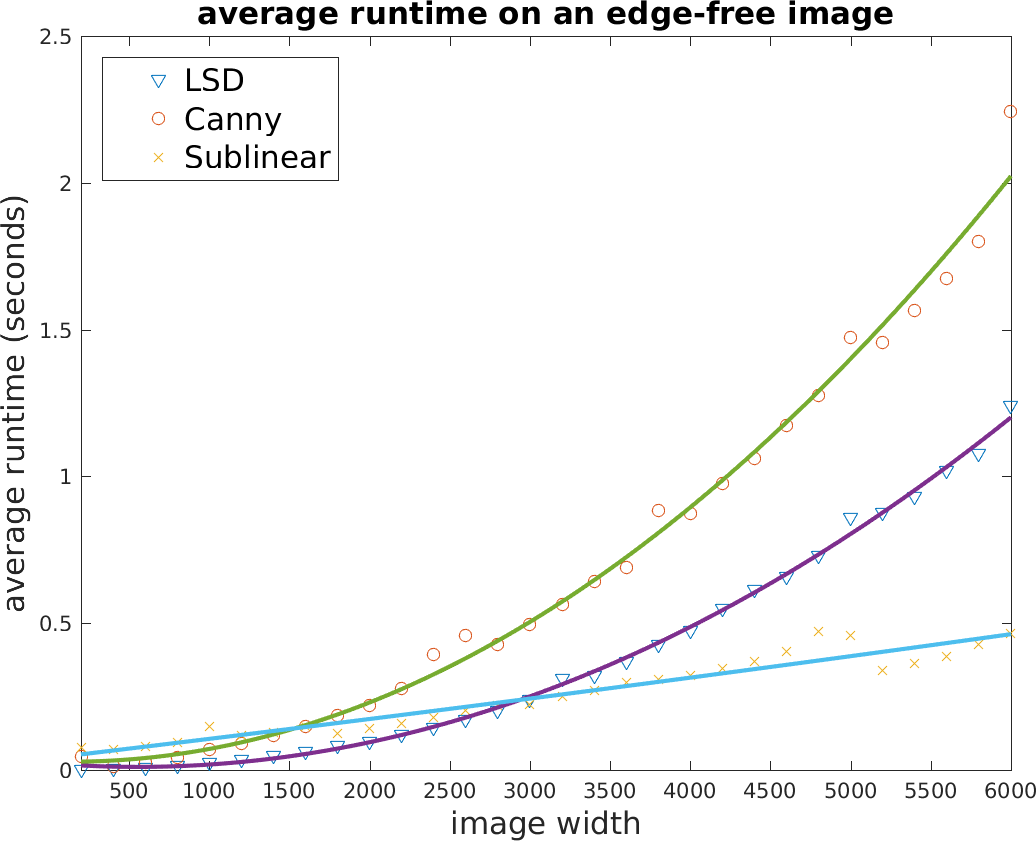
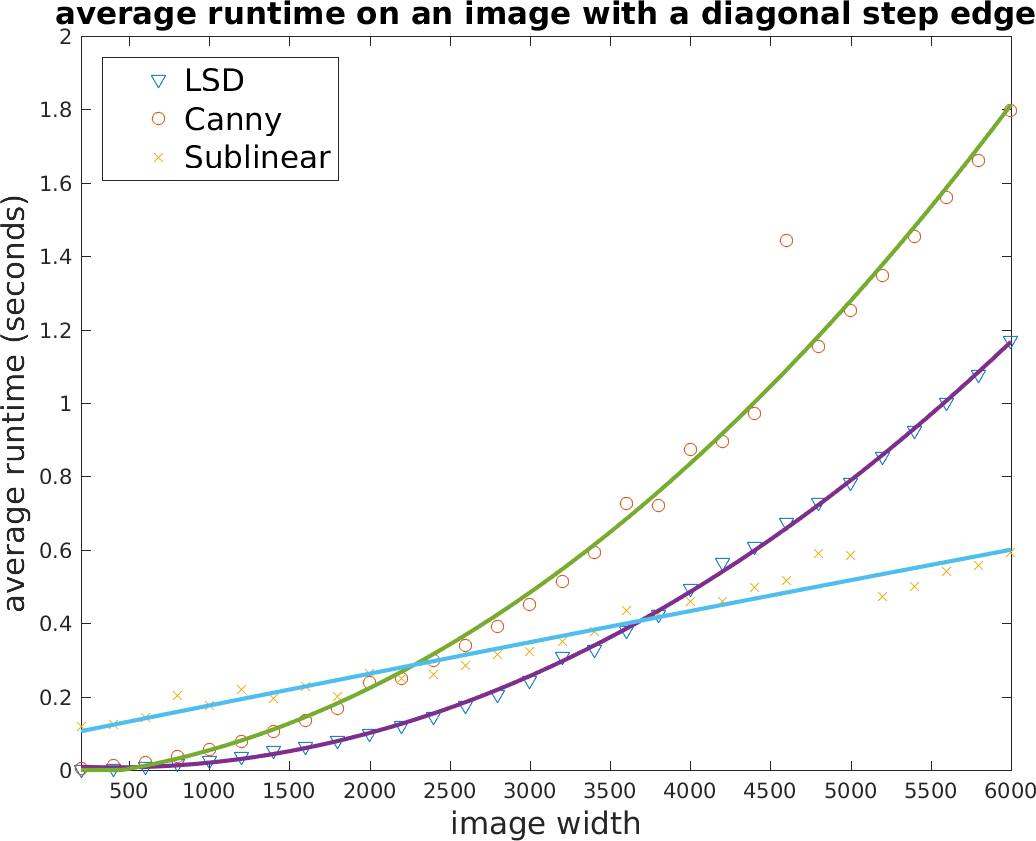
Finally, the runtime of three algorithms were compared on two sequences of synthetic square images of increasing sizes. The first sequence contained pure noise and as a result, the tracking algorithm did not run. In the second sequence, however, the images contained one step edge, both detection and tracking would run. The two figures below thus show that (a) tracking is significantly faster than detection and (b) our algorithm ran indeed in sublinear time, both in agreement with our theoretical analysis in [1].

5. Code

A matlab implementation of our method can be found here.
The zip-file contains the following directories:

images - Several test images including those displayed in the manuscript.
curved_sublinear - Includes a demo file and scripts that reproduce the figures in [1].
LSD - Implementation of the Line Segment Detector method [4] downloaded from [5].

See demo.m and the help of the routine itself for instructions how to use it.

6. References

Y.-Q. Wang, A. Trouve, Y. Amit and B. Nadler, Detecting curved edges in noisy images in sublinear time, 2016.
I. Horev, B. Nadler, E. Arias-Castro, M. Galun and R. Basri, Detection of Long Edges on a Computational Budget: A Sublinear Approach , SIAM Journal of Imaging Sciences, vol. 8, no. 1., pp. 458-483, 2015.
J. Canny, A computational approach to edge detection , IEEE Trans. Pattern Anal. Mach. Intell., 8 (1986), pp. 679-698.
R.G. von Gioi, J. Jakubowicz, J.M. Morel, and G. Randall, LSD: A fast line segment detector with a false detection control , IEEE Trans. Pattern Anal. Mach. Intell., 32 (2010), pp. 722-732.
R.G. von Gioi, J. Jakubowicz, J.M. Morel, and G. Randall, LSD: A Line Segment Detector , IPOL, 2 (2012), pp. 35-55; available online at http://dx.doi.org/10.5201/ipol.2012.gjmr-lsd.
M. Lebrun, M. Colom, A. Buades, and J.M. Morel, Secrets of image denoising cuisine , Acta Numer., 21 (2012), pp. 475-576.
C. Liu, W. T. Freeman, R. Szeliski, and S. B. Kang, Noise estimation from a single image, , Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2006, pp. 901-908.

Curved Edge Detection in Sublinear Time
Oct. 2016

1. Introduction

Fig. 1 - An $1024 \times 768$ image depicting lanes under poor visibility conditions. The fog reduces contrast and leads to occasionally barely visible edges.

2. Problem Setup

Fig. 2 - a piecewise constant image with two curved step edges and three equidistant strips.

3. A Sublinear Approach to Curved Edge Detection

Fig. 3 - Illustration of our approach: (a) the noisy synthetic $1000 \times 1000$ image (SNR=0.5); (b) detected edges in the strip delimited by blue columns; (c) output of the first tracking iteration; (d) fully-tracked edge estimates.

4. Results

Fig. 4 - Curved edge detection under different SNRs. Here two strips (one horizontal and one vertical) were extracted from the inputs for detecting edges.

5. Code

6. References

Curved Edge Detection in Sublinear Time Oct. 2016

1. Introduction

Fig. 1 - An 1024×7681000×10001024 \times 768image depicting lanes under poor visibility conditions. The fog reduces contrast and leads to occasionally barely visible edges.

2. Problem Setup

Fig. 2 - a piecewise constant image with two curved step edges and three equidistant strips.

3. A Sublinear Approach to Curved Edge Detection

Fig. 3 - Illustration of our approach: (a) the noisy synthetic 1000×10001000×10001000 \times 1000 image (SNR=0.5); (b) detected edges in the strip delimited by blue columns; (c) output of the first tracking iteration; (d) fully-tracked edge estimates.

4. Results

Fig. 4 - Curved edge detection under different SNRs. Here two strips (one horizontal and one vertical) were extracted from the inputs for detecting edges.

5. Code

6. References

Curved Edge Detection in Sublinear Time
Oct. 2016

Fig. 1 - An $1024 \times 768$ image depicting lanes under poor visibility conditions. The fog reduces contrast and leads to occasionally barely visible edges.

Fig. 3 - Illustration of our approach: (a) the noisy synthetic $1000 \times 1000$ image (SNR=0.5); (b) detected edges in the strip delimited by blue columns; (c) output of the first tracking iteration; (d) fully-tracked edge estimates.