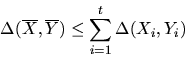Oded Goldreich
Some Useful Trivial Tricks
under construction...
Following are some useful trivialities regarding randomness and computations.
Although trivial,
these tricks are often useful in avoiding irrelevant technicalities.
Statistical Distance
The statistical distance between two random variables $X$ and $Y$,
denoted $DELTA(X,Y)$, can be defined in two equivalent ways:
(1) half of the sum of the absolute value of the pointwise distances,
and (2) the maximum discrepency between the probability of some event.
That is,
In some situations one of these definitions is more convenient
to work with than the other.
The following trivial facts are useful.
- Statistical distance satisfies the triangle inequality.
[This is easily proved by using the forst definition.]
- For every randomized process $Pi$ it holds that
$DELTA(Pi(X),Pi(Y))$ is upper-bounded by $DELTA(X,Y)$.
[This is easily proved by using the second definition.]
- For sequences of independent random variables
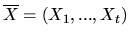 and
and
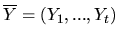 it holds that
it holds that
Note the inequality may not hold in case the sequences are
dependent (e.g., consider the sequences $(X,X)$ and $(X,Y)$,
where $X$ and $Y$ are independent identically distributed variables).
Defining security
In many definitions the adversary is given the security paramter
in unary, in order to allow it to run in time polynomial in that
parameter. An alternative convention postulates that the objects
considered with security paramter $n$ have length that is polynomially
related to $n$ (and that $n$ can be efficiently reconstructed from
their length). Tyically, this convention may be enforced by replacing
the object $x$ by the augmented object $x'=(1^n,x)$.
Computational Indistinguishability
- Computational indistinguishability satisfies the triangle inequality.
- If the ensembles $(X_n)$ and $(Y_n)$
are computationally indistinguishable
then for every probabilistic polynomial-time algorithm $A$
the ensembles $(A(X_n))$ and $(A(Y_n))$
are computationally indistinguishable.
Zero-Knowledge
-
When analyzing a simulator (for a zero-knowledge proof system)
one may typically assume that the simulator always
outputs accepted conversations.
That is, whenever the simulator outputs a non-accepting conversation
(which may happen quite often only in case the input is not in the
language),
the modified simulator can replace it by a fixed accepting
conversation
(which is typically easy to generate; or else one may consider a minor
modification of the verifier for which this holds).
-
When constructing a (black-box) simulator it suffices
to consider deterministic cheating verifiers.
This will guarantee proper simulation of probabilistic verifiers
for each possible setting of their random-tape.
Probablistic Proof Systems
-
Shifting error between soundness and completeness.
Suppose you obtain a proof system with completeness error $\epsilon$
and soundness error $0.5+\epsilon$. Then, by a trivial modification,
you can obtain a proof system with completeness error $O(\epsilon)$
and soundness error $0.5$.
Back to
Oded Goldreich's homepage.
![\begin{eqnarray*}\Delta(X,Y)
&=& \frac12\cdot\sum_v\vert{\sf Pr}[X=v]-{\sf Pr}[Y=v]\vert \\
&=& \max_{S}\{{\sf Pr}[X\in S]-{\sf Pr}[Y\in S]\} \end{eqnarray*}](tricks-img1.gif)
![\begin{eqnarray*}\Delta(X,Y)
&=& \frac12\cdot\sum_v\vert{\sf Pr}[X=v]-{\sf Pr}[Y=v]\vert \\
&=& \max_{S}\{{\sf Pr}[X\in S]-{\sf Pr}[Y\in S]\} \end{eqnarray*}](tricks-img1.gif)