Milestone Year
1991
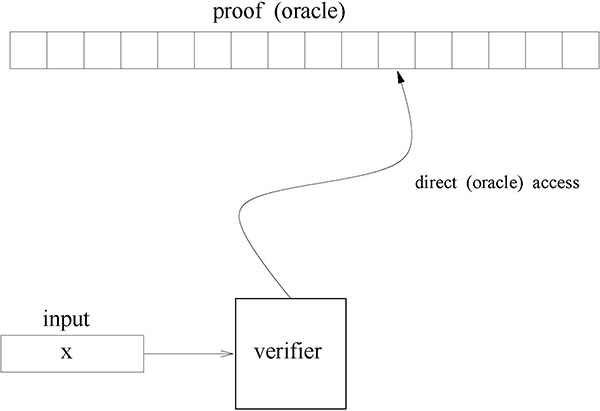
PCP: Locally (and Probabilistically) Checkable Proofs
WIS scientists and their collaborators showed that proofs can be transformed into a redundant form that allows probabilistic verification based on probing the alleged proof in very few locations; specifically, the number of probed locations may be polylogarithmic in the length of the assertion being proved. They also showed a connection between this model of proofs (later termed PCPs) and the hardness of approximating some natural combinatorial parameters (i.e., the maximum clique size in a graph). This connection has revolutionized the study of the complexity of approximation problems by offering a new avenue for establishing strong intractability results.
The PCP model is closely related to another model of proof systems that was proposed by a WIS scientist and her collaborators in 1988; specifically, the model of multi-prover interactive proofs.
In general, WIS scientists made numerous important contributions to the study of PCP and the hardness of approximating natural combinatorial parameters. Notable examples include Parallel Repetition and PCP.