|
Data-Dependent MLS for Faithful Surface Approximation |
|
|
|
|
|
|
|
|
|
|
|
Abstract: |
|
|
|
In this paper we present a high-fidelity surface approximation technique that aims at a faithful reconstruction of piecewise-smooth surfaces from a scattered point set. The presented method builds on the Moving Least-Squares (MLS) projection methodology, but introduces a fundamental modification: While the classical MLS uses a fixed approximation space, i.e., polynomials of a certain degree, the new method is data-dependent. For each projected point, it finds a proper local approximation space of piecewise polynomials (splines). The locally constructed spline encapsulates the local singularities which may exist in the data. The optional singularity for this local approximation space is modeled via a Singularity Indicator Field (SIF) which is computed over the input data points. We demonstrate the effectiveness of the method by reconstructing surfaces from real scanned 3D data, while being faithful to their most delicate features. |
|
|
|
Technical Report: |
|
|
|
|
|
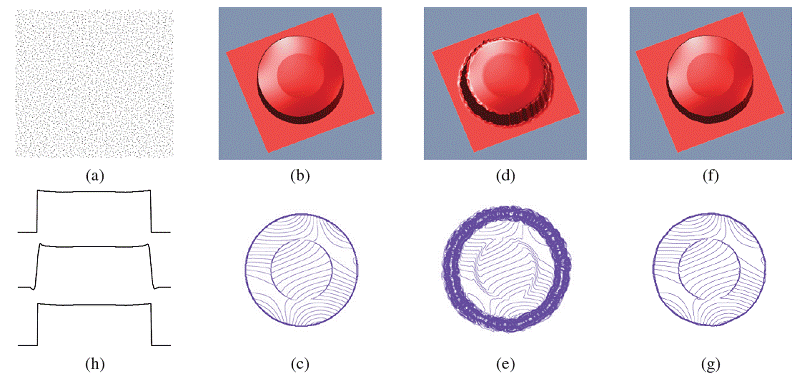
The height function in (b) contains two types of circular features. Across the outer circle there is a function discontinuity, and across the inner circle there is a delicate derivative discontinuity. The data set consists of the irregular point samples (a). (d) and (f) demonstrate reconstruction by MLS and DDMLS, respectively. To better visualize the Gibbs phenomenon and the over-smoothing, the corresponding isophote lines are presented at the bottom row. Note the oscillations near the boundaries and the smoothing effect of the delicate inner circular feature caused by the MLS, compared with the faithfulness of the DDMLS. To further illustrates the effect, 1D slices of the original, MLS, and DDMLS are displayed in (h) from top to bottom. |
|
|
|
|
|
|
|
A scanned soap. (a) shows the ground truth (photograph). In (b) pct is taken as the 100th percentile, i.e., regular MLS. In (c) and (d) pct is taken as the 90th and the 75th percentile, respectively. Note how the fine scratch on the soap (marked by small arrow) is reconstructed by the DDMLS and smoothed out by the MLS. The small upper window at (a) shows a portion of the scanned point cloud. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|