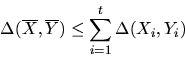Oded Goldreich

Some Useful Trivial Tricks

under construction...

Following are some useful trivialities regarding randomness and computations. Although trivial, these tricks are often useful in avoiding irrelevant technicalities.

Statistical Distance

The statistical distance between two random variables $X$ and $Y$, denoted $DELTA(X,Y)$, can be defined in two equivalent ways: (1) half of the sum of the absolute value of the pointwise distances, and (2) the maximum discrepency between the probability of some event. That is,

$\begin{eqnarray*}\Delta(X,Y) &=& \frac12\cdot\sum_v\vert{\sf Pr}[X=v]-{\sf Pr}[Y=v]\vert \\ &=& \max_{S}\{{\sf Pr}[X\in S]-{\sf Pr}[Y\in S]\} \end{eqnarray*}$

In some situations one of these definitions is more convenient to work with than the other. The following trivial facts are useful.

Statistical distance satisfies the triangle inequality. [This is easily proved by using the forst definition.]
For every randomized process $Pi$ it holds that $DELTA(Pi(X),Pi(Y))$ is upper-bounded by $DELTA(X,Y)$. [This is easily proved by using the second definition.]
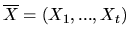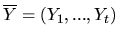For sequences of independent random variables ${\overline X}=(X_1,...,X_t)$ and ${\overline Y}=(Y_1,...,Y_t)$ it holds that

$\begin{displaymath}\Delta({\overline X},{\overline Y}) \leq \sum_{i=1}^t \Delta(X_i,Y_i)\end{displaymath}$

Note the inequality may not hold in case the sequences are dependent (e.g., consider the sequences $(X,X)$ and $(X,Y)$, where $X$ and $Y$ are independent identically distributed variables).

Defining security

In many definitions the adversary is given the security paramter in unary, in order to allow it to run in time polynomial in that parameter. An alternative convention postulates that the objects considered with security paramter $n$ have length that is polynomially related to $n$ (and that $n$ can be efficiently reconstructed from their length). Tyically, this convention may be enforced by replacing the object $x$ by the augmented object $x'=(1^n,x)$.

Computational Indistinguishability

Computational indistinguishability satisfies the triangle inequality.
If the ensembles $(X_n)$ and $(Y_n)$ are computationally indistinguishable then for every probabilistic polynomial-time algorithm $A$ the ensembles $(A(X_n))$ and $(A(Y_n))$ are computationally indistinguishable.

Zero-Knowledge

When analyzing a simulator (for a zero-knowledge proof system) one may typically assume that the simulator always outputs accepted conversations. That is, whenever the simulator outputs a non-accepting conversation (which may happen quite often only in case the input is not in the language), the modified simulator can replace it by a fixed accepting conversation (which is typically easy to generate; or else one may consider a minor modification of the verifier for which this holds).
When constructing a (black-box) simulator it suffices to consider deterministic cheating verifiers. This will guarantee proper simulation of probabilistic verifiers for each possible setting of their random-tape.

Probablistic Proof Systems

Shifting error between soundness and completeness. Suppose you obtain a proof system with completeness error $\epsilon$ and soundness error $0.5+\epsilon$. Then, by a trivial modification, you can obtain a proof system with completeness error $O(\epsilon)$ and soundness error $0.5$.

Back to Oded Goldreich's homepage.