
Detection of edges in images is a fundamental task in image analysis, with many edge detection algorithms developed over the past 30 years. While edges may be defined in several ways, in this work we assumed the classical model of step discontinuities. One of the most common algorithms to detect such edges is [2] . A more recent method, aimed at straight edges is the Line Segment Detector (LSD) [3] . Both of these methods are relatively fast with a run-time linear in the number of image pixels, but perform well only at low noise levels.

In various applications, however, there is a need for
edge detection methods that are both fast and robust to noise.
In some of these applications the images are taken
under poor visibility conditions, such as extreme fog as in Fig. 1 above.
Furthermore, the images are typically acquired and stored by hardware,
such as a CCD camera, and
the requirement of real-time processing may restrict their transfer from memory to CPU
and subsequent analysis to only a fraction of all image pixels.
This motivates the following question:
How well can one detect edges in noisy images under severe computational constraints?
In this page and the accompanying paper [1] we present a novel algorithm for extremely efficient detection of long straight edges with complexity that is sub-linear in the total number of image pixels. The key idea underlying our approach is that to detect long edges, it is not necessary to process all image pixels, but rather only a small subset.
Let $I_c(x,y)$ be a noise-free function defined on a rectangular domain $\Omega \subset \mathbb{R}^2$. As a simple image formation model, let $I$ be the discrete image of size $n_x \times n_y$ pixels, obtained by ideal sampling of $I_c$ (with a $\delta$ point spread function) on a uniform rectangular grid, and corrupted by additive noise \begin{equation} I_{i,j} = I_c(h_x \cdot i, h_y \cdot j) + \xi_{i,j}. \end{equation} For simplicity, we assume that the noise is i.i.d. Gaussian, $\xi_{i,j} \sim N(0,\sigma^2)$ with known variance $\sigma^2$, and independent of $I_c$. When $\sigma$ is unknown, it can be estimated from the image (see [6] ,[7] for a review of noise estimation methods). Finally, in what follows, for notational clarity we consider square images with $n_x = n_y = n$.
The key question we consider is how well can edge detection be done under computational constraints, in particular with sub-linear time complexity. We study this problem under the following simplified image model: the noise-free function $I_c$ is piece-wise constant, with constant values in different regions $\Omega_i\subset \Omega$. The boundaries between adjacent regions $\Omega_i$ delineate long and straight edges $\Gamma_i$. Note that we make no assumptions on the sizes or shapes of the regions $\Omega_i$. For example, some may be thin fibers at arbitrary locations and orientations.
Given the noisy image $I$, our goal is to detect and localize the long and straight edges in it, with a time complexity sub-linear in the number of image pixels. In particular, we present an algorithm that initially samples only $O(n^\beta)$ of all image pixels for some $\beta < 2$.
To detect horizontal edges, making an angle of up to 45 degrees with the $x$-axis, we sample several vertical strips of pixels. To detect vertical edges, we apply our algorithm to the transposed image. For simplicity, we here describe the basic algorithm, which does not deal with advanced issues such as non-maximal suppression and improved edge localization. For more details, see sections 3-5 of [1] .
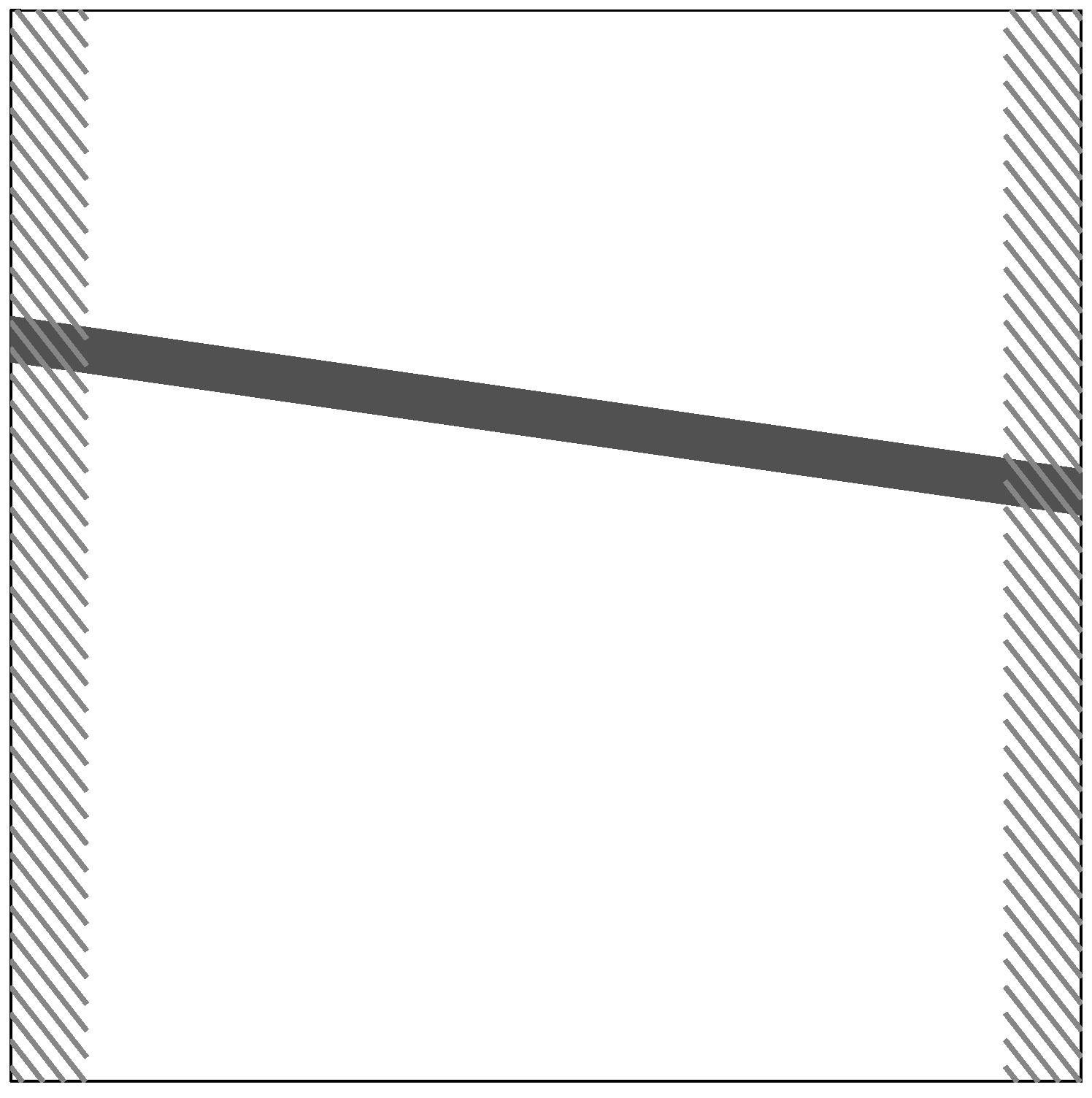
Input
Output
Algorithm:
We compared our algorithm to the Canny Edge Detector [2] , the Line Segment Detector (LSD) [3] , and the Straight Edge Detector [5] , on simulated, natural, and electron microscope images. Here, we present only a some of our results. For the rest, see [1] .
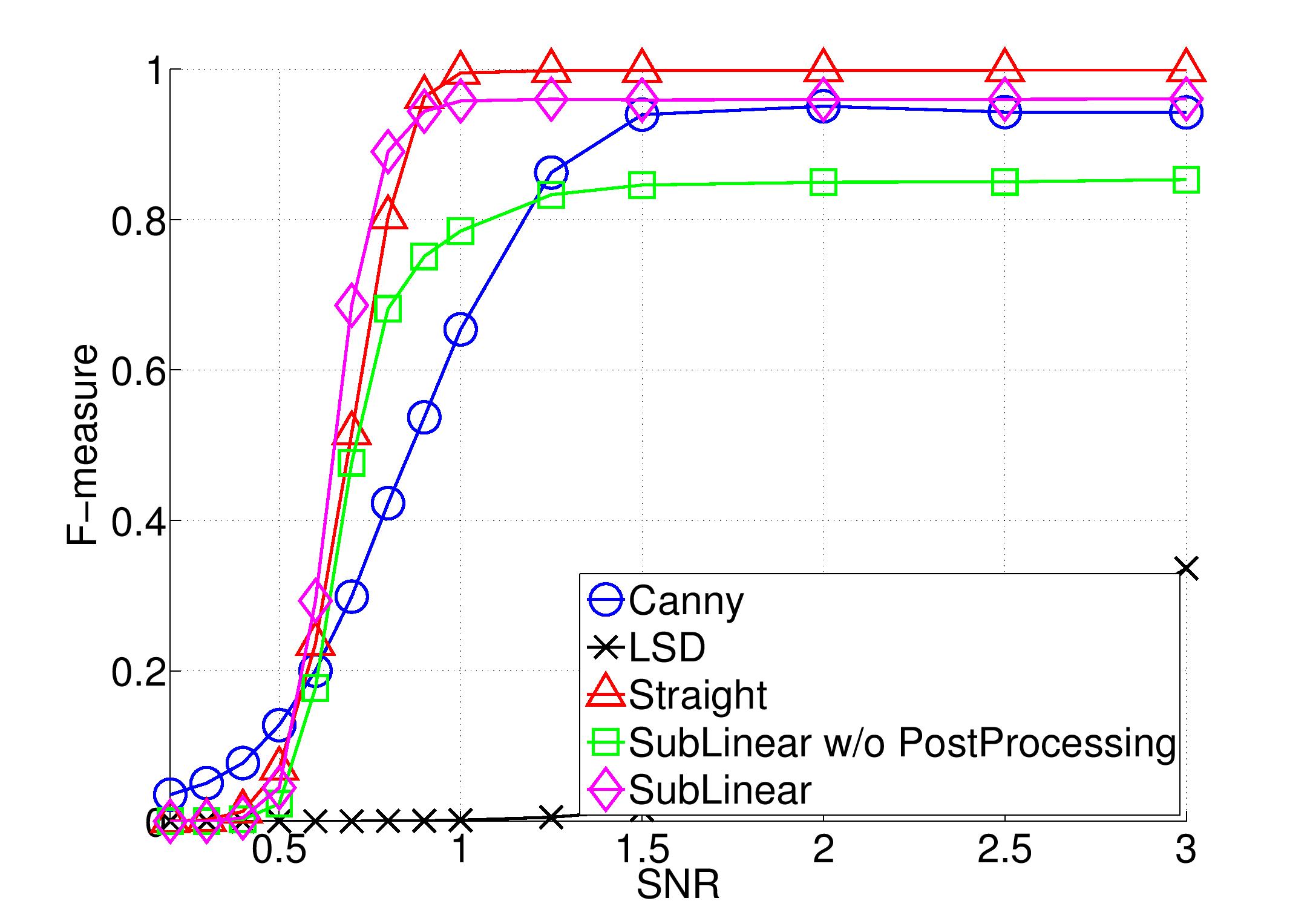
On the simulated image, for which the ground truth is known, all algorithms were evaluated quantitatively by means of the F-measure for image segmentation as described in [8] . The F-measure is defined as the harmonic mean between two quantities, recall and precision, and is thus a number between 0 and 1 with a value of 1 representing perfect detection. Recall is the fraction of true edge pixels that are detected, whereas precision is the fraction of edge pixel detections that are indeed true positives rather than false positives. In the context of edge detection, the particular F-measure of [8] allows for some small tolerance in the localization of the edges; see that paper for exact details.
For the quantitative comparison, a clean synthetic image of size $1000 \times 1000$ (see Figure 3(a)), was corrupted by noise of varying strength, yielding SNRs in the range $[0.2, 3]$. Figure 3(b) shows the F-measure as a function of the SNR for the various methods, averaged over 25 iterations. For a discussion of the results, see [1] .
We note that on a standard desktop PC, both Canny and LSD took about 0.5sec to process this $1000 \times 1000$ image. The Straight Edge Detector, although far more accurate, took about 50sec, whereas our sublinear algorithm had a run-time of 1.6sec.
Next, we include some results on natural images:




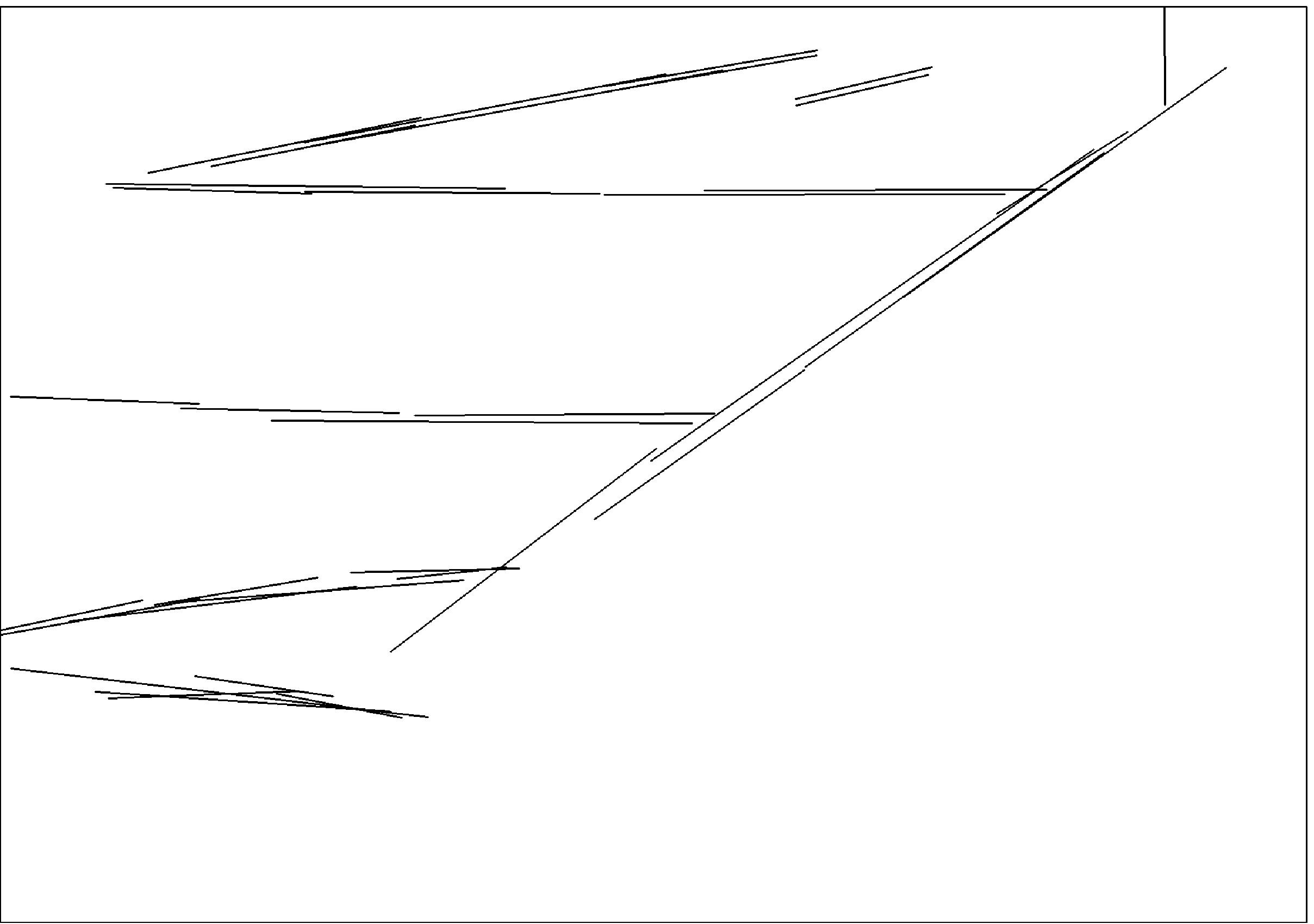


A matlab implementation of our method can be found here.
The zip-file contains the following directories:
The main procedure, inside the Sublinear directory is sublinear_edge_detection.m
See demo.m and the help of the routine itself for instructions how to use it.
J. Canny, A computational approach to edge detection , IEEE Trans. Pattern Anal. Mach. Intell., 8 (1986), pp. 679-698.
R.G. von Gioi, J. Jakubowicz, J.M. Morel, and G. Randall, LSD: A fast line segment detector with a false detection control , IEEE Trans. Pattern Anal. Mach. Intell., 32 (2010), pp. 722-732.
R.G. von Gioi, J. Jakubowicz, J.M. Morel, and G. Randall, LSD: A Line Segment Detector , IPOL, 2 (2012), pp. 35-55; available online at http://dx.doi.org/10.5201/ipol.2012.gjmr-lsd.
M. Galun, R. Basri, and A. Brandt, Multiscale edge detection and ber enhancement using differences of oriented means , in Proceedings of the IEEE 11th International Conference on Computer Vision, 2007.
M. Lebrun, M. Colom, A. Buades, and J.M. Morel, Secrets of image denoising cuisine , Acta Numer., 21 (2012), pp. 475-576.
C. Liu, W. T. Freeman, R. Szeliski, and S. B. Kang, Noise estimation from a single image, , Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2006, pp. 901-908.
D. R. Martin, C. C. Fowlkes, and J. Malik, Learning to detect natural image boundaries using local brightness, color, and texture cues, , IEEE Trans. Pattern Anal. Mach. Intell., 26 (2004), pp. 530-549.