|
|
Milestone Year
2008
A Constructive Solution to the Infinitesimal Hilbert 16th Problem
In 1901, the famous mathematician David Hilbert suggested 23 problems as main mathematical challenges for the 20th century. During the next century all but two of these problems were solved. One of the diehards is the Riemann hypothesis on zeros of the zeta function, and the other is (the second half of) the 16th problem, on limit cycles of polynomial vector fields.
In the first part of this problem, Hilbert asks about the number and possible relative position of algebraic ovals on the plane, which are closed curves defined by one polynomial equation. This problem triggered the creation of a new branch of mathematics, and eventually the algebraic question was answered.
In the second part, Hilbert asks ``the same question about limit cycles of a differential equation'', which are closed curves defined by differential (rather than algebraic) equations with polynomial right hand sides. A century of efforts yielded answers only for the case of degree 2 (whereas differential equations of degree 1 have no limit cycles): It is known that differential equations of degree 2 may have any number of limit cycles (but no explicit examples with 5 or more cycles are known) and that each particular equation may have at most finitely many such cycles.
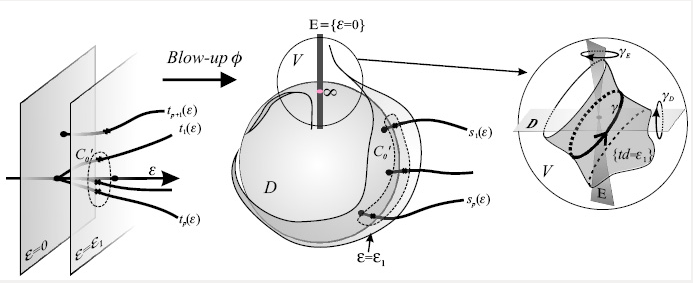
Challenged by this unyielding problem, mathematicians tried to deal first with relaxed versions of the original question. In particular, they tried to study limit cycles born from algebraic ovals (like in the first part of the problem) by small perturbation. Such formulation first appeared in the late 1960-ies, but it also turned out very hard: Intensive efforts in the subsequent decades yielded only partial results on the asymptotic behavior with unknown constants. In particular, no explicit bound was know for the case of degree 5 and higher.
A fully constructive solution was achieved only in 2008, when WIS scientists
provided an explicit double exponential bound of
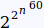where n is the degree of the polynomial right hand sides of the equation.
