On the Complexity of Statistical Reasoning
Joe Kilian and Moni Naor
Abstract:
We show that basic problems in reasoning about statistics are
NP-hard to even approximately solve.
We consider the problem of detecting internal inconsistencies in a set
of statistics. We say that a set of statistics is
 -inconsistent if one of the probabilities must be off by at
least
-inconsistent if one of the probabilities must be off by at
least  . For a positive constant
. For a positive constant  , We show
that it is NP-hard to distinguish
, We show
that it is NP-hard to distinguish  -inconsistent statistics from
self-consistent statistics. This result holds when restricted to
complete sets of pairwise statistics over Boolean domains.
-inconsistent statistics from
self-consistent statistics. This result holds when restricted to
complete sets of pairwise statistics over Boolean domains.
We next consider what may be determined about distributions with a
given (consistent) set of pairwise statistics over Boolean domains.
We show that it is NP-hard to distinguish between the case that
 is necessarily 0 and the case that
is necessarily 0 and the case that 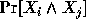 can have any value in
can have any value in  . Similarly, we show it
NP-hard to distinguish between the case that
. Similarly, we show it
NP-hard to distinguish between the case that  and the case that
and the case that  is unconstrained.
is unconstrained.
Whereas the connection between PCP and hardness of approximations has
been known for a while,
we introduce the
application of ``zero-knowledge'' PCP's as a tool for proving
NP-hardness results for approximation problems.
Postscript
, gzipped Postscript .
Back to On-Line Publications
Back Home
 -inconsistent if one of the probabilities must be off by at
least
-inconsistent if one of the probabilities must be off by at
least  . For a positive constant
. For a positive constant  , We show
that it is NP-hard to distinguish
, We show
that it is NP-hard to distinguish  -inconsistent statistics from
self-consistent statistics. This result holds when restricted to
complete sets of pairwise statistics over Boolean domains.
-inconsistent statistics from
self-consistent statistics. This result holds when restricted to
complete sets of pairwise statistics over Boolean domains.
 is necessarily 0 and the case that
is necessarily 0 and the case that 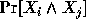 can have any value in
can have any value in  . Similarly, we show it
NP-hard to distinguish between the case that
. Similarly, we show it
NP-hard to distinguish between the case that  and the case that
and the case that  is unconstrained.
is unconstrained.