Milestone Year
1986
A new geometry
The spaces studied in classical mathematics are inextricably linked to real
and complex numbers. For example, points of Euclidean spaces are described
by their coordinates of real numbers.
At the end of nineteenth century, Kurt Hensel discovered that
the field of rational numbers can be embedded in infinitely many fields
of a different type, called the fields of p-adic numbers.
Each of them is related to one prime number p,
which determines a different distance between rational numbers.
In the second half of twentieth century, number theory
dictated the necessity to find what p-adic analogs
of the classical spaces, e.g., complex analytic ones, are.
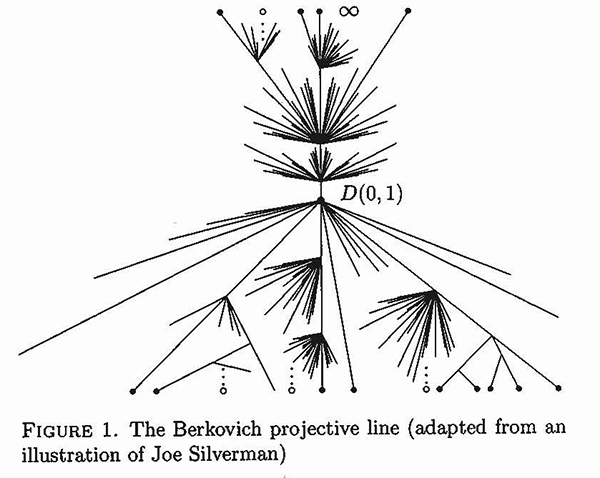
The difficulty of this problem lies in the fact that the fields of p-adic numbers are totally disconnected. In particular, the space, whose points are described by coordinates of p-adic numbers in the same way as points of the Euclidean spaces, is also totally disconnected; hence, it is not an actual geometrical object.
In 1986, a WIS scientist found a way to define analytic spaces over p-adic numbers. In comparison to what was introduced earlier, they provided genuine geometrical objects which are as good as their classical analogs. But while the one-dimensional space based on real numbers is a simple real line, the one-dimensional space based on p-adic numbers is an infinitely branching tree.
The new spaces were used to solve important problems in number theory and algebraic geometry. Besides they are used in other areas of mathematics and mathematical physics such as dynamical systems, potential theory, complex analytic geometry, tropical geometry, and mirror symmetry.