Milestone Year
1986
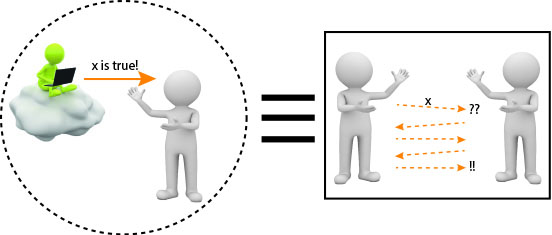
Zero-Knowledge: Proofs that yield nothing but their validity
In cryptographic settings, parties are often requested to take
predetermined actions based on their secrets.
This raised the question of how can we verify that these
parties actually acted correctly, without asking them
to reveal their secrets?
This general problem is addressed by the notion of zero-knowledge proofs:
These are proofs that establish the validity of their assertion
without revealing any additional information,
Thus, using a zero-knowledge proof, a party can prove that it has acted
according to the predetermined instructions without leaking any
additional information about its secrets.
Zero-knowledge proofs for non-trivial assertions are necessarily
interactive and randomized (see Interactive proofs). They were first suggested
by a WIS scientist and her collaborators in 1983,
and their wide applicability was demonstrated
by a WIS scientist and his collaborators in 1986.
In particular, based on standard intractability assumptions
(like the intractability of factoring large integers),
it was shown how to convert any proof system into a zero-knowledge one.
Subsequently, WIS scientists made numerous important contributions to the study of zero-knowledge.