An Implementation of Efficient Pseudo-Random Functions
Michael Langberg
Tue Mar 31 16:55:21 IDT 1998
Abstract
Naor and Reingold [3] have recently introduced two new constructions of
very efficient pseudo-random functions, proven to be as secure as the decisional
version of the Diffie-Hellman [2] assumption or the assumption that
factoring is hard.
In this site we define and exhibit an implementation of the construction
which is based on the decisional Diffie-Hellman assumption.
Naor and Reingold define a pseudo-random function 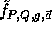 as follows:
The key of each pseudo-random function is a tuple,
as follows:
The key of each pseudo-random function is a tuple, 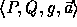 ,
where P is a large prime, Q a large prime divisor of P-1,
g an element of order Q in
,
where P is a large prime, Q a large prime divisor of P-1,
g an element of order Q in 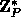 and
and 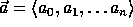 a uniformly distributed sequence of n+1 elements in
a uniformly distributed sequence of n+1 elements in 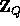 .
For any n-bit input,
.
For any n-bit input,
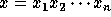 , the function
, the function 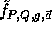 is defined by:
is defined by:
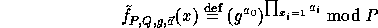
This function is the core of our implementation.
The function 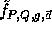 has domain
has domain 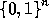 and range
and range
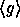 (the subgroup of
(the subgroup of 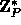 generated by g).
We now show how to adjust
generated by g).
We now show how to adjust 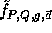 in order to get a
in order to get a 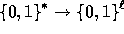 pseudo-random function.
I.e., the input of the function is a bit string of arbitrary
length and the output is a pseudo-random bit string of fixed length
pseudo-random function.
I.e., the input of the function is a bit string of arbitrary
length and the output is a pseudo-random bit string of fixed length 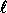 (instead of a pseudo-random element in
(instead of a pseudo-random element in 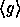 ).
For every input
).
For every input 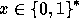 the function
the function
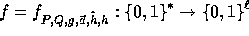 we implement is
defined by:
we implement is
defined by:
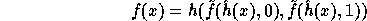
where
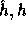 are two hash functions (defined below) and
are two hash functions (defined below) and 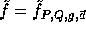 .
In words, the computation of f is as follows: First apply
.
In words, the computation of f is as follows: First apply 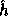 on the input
to get
on the input
to get 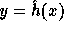 . Then compute two pseudo-random elements
. Then compute two pseudo-random elements 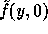 and
and 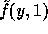 in
in 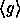 . Finally concatenate these elements
and hash the outcome by the second hash function h.
. Finally concatenate these elements
and hash the outcome by the second hash function h.
The first step in the computation of f is hashing the input 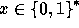 to
receive an element
to
receive an element 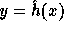 s.t.
s.t. 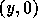 and
and 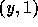 are in the domain of
the pseudo-random function
are in the domain of
the pseudo-random function 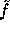 . In order for
. In order for 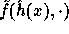 to be pseudo-random it is enough to require that for any two different inputs
to be pseudo-random it is enough to require that for any two different inputs
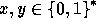 the probability of collision,
the probability of collision,
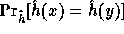 , is negligible.
To get this we define
, is negligible.
To get this we define 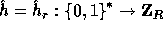 as follows:
as follows:
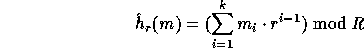
where R is a 161-bit prime, r (the key of 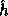 ) is a uniformly distributed
element in
) is a uniformly distributed
element in 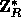 and the input m is partitioned into a sequence,
and the input m is partitioned into a sequence,
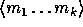 , of elements in
, of elements in 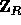 .
With this definition the collision probability on any two inputs of length at
most 160k is bounded by
.
With this definition the collision probability on any two inputs of length at
most 160k is bounded by 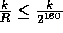 . The probability
of collision for some pair of inputs among
. The probability
of collision for some pair of inputs among 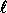 arbitrarily chosen inputs
is bounded by
arbitrarily chosen inputs
is bounded by 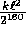 . For practical
values of
. For practical
values of 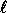 and k this probability is sufficiently small.
and k this probability is sufficiently small.
As mentioned above, on input 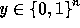 our core function
our core function 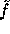 will
output a pseudo-random element in the subgroup
will
output a pseudo-random element in the subgroup 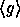 . Converting this
element into a pseudo-random value in
. Converting this
element into a pseudo-random value in 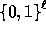 is done using a second hash
function
is done using a second hash
function 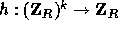 . The requirement from
h is that for any pair of different inputs x,y the collision probability
. The requirement from
h is that for any pair of different inputs x,y the collision probability
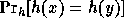 is
is 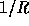 (or ``extremely close'' to this value).
Therefore, we cannot define
(or ``extremely close'' to this value).
Therefore, we cannot define 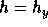 in the same way we defined
in the same way we defined 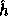 .
Rather than that we use the following definition:
.
Rather than that we use the following definition:
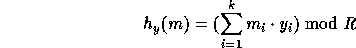
where R is a 161-bit prime (as above), 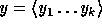 (the key of
(the key of 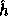 ) is a uniformly distributed sequence of elements in
) is a uniformly distributed sequence of elements in 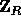 and the input
and the input 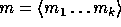 is a sequence
of elements in
is a sequence
of elements in 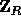 .
.
With this definition of h we can conclude from [3] that if X
is a random variable uniformly distributed over a set of size 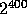 ,
then for all but a fraction
,
then for all but a fraction 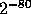 of the choices of y
the random variable
of the choices of y
the random variable 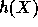 is of statistical distance at most
is of statistical distance at most 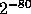 from the uniform distribution over
from the uniform distribution over 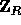 .
Therefore, if X is a pseudo-random element in such a set then (for all but
a fraction
.
Therefore, if X is a pseudo-random element in such a set then (for all but
a fraction 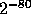 of the choices of y) the random variable
of the choices of y) the random variable 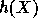 is a pseudo-random value in
is a pseudo-random value in 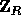 . Note that choosing R extremely close to
. Note that choosing R extremely close to 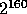 guarantees
guarantees 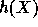 to be
pseudo-random in
to be
pseudo-random in 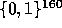 .
In our case, for any
.
In our case, for any 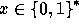 the value
the value 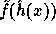 is pseudo-random
in
is pseudo-random
in 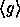 . Thus if we fix
. Thus if we fix 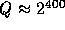 (implying the size of
(implying the size of 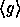 to be
to be 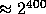 ) we can define our pseudo-random function as
) we can define our pseudo-random function as
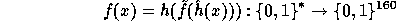
However, defining Q of size 400 bits seems to be an overkill (in terms of
security) and leads to an inefficient implementation. We therefore use
the following optimization: We define Q of size 200 bits and on input
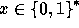 we compute the element
we compute the element
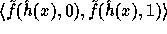 which is
pseudo-random in
which is
pseudo-random in  .
Since
.
Since 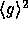 is of size approximately
is of size approximately 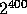 , we define
, we define
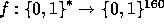 (by the previous analysis) to be
(by the previous analysis) to be
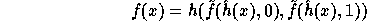
This suggestion is more efficient than the previous one since the exponent of g
in the computation of 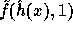 can be derived from the
exponent of g in the computation of
can be derived from the
exponent of g in the computation of 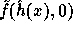 using a
single modular multiplication.
using a
single modular multiplication.
In our discussion so far we assumed that 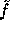 is a pseudo-random function.
As shown by Naor and Reingold, this is true as long as the decisional
version of the Diffie-Hellman assumption holds. In the current state of knowledge
it seems that choosing P of 1000 bits and Q of 200 bits makes this
assumption sufficiently safe.
is a pseudo-random function.
As shown by Naor and Reingold, this is true as long as the decisional
version of the Diffie-Hellman assumption holds. In the current state of knowledge
it seems that choosing P of 1000 bits and Q of 200 bits makes this
assumption sufficiently safe.
The specific constants used in our implementation are:
-
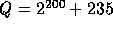 ,
, 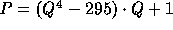 .
.
-
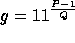 .
.
- n = 160.
-
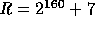 .
.
For all computations and primality checks involving large numbers we used the
NTL package [4] by V. Shoup.
In this implementation the key 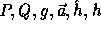 was generated
as follows:
was generated
as follows:
In order to define 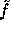 , we need two large primes P,Q s.t.
, we need two large primes P,Q s.t. 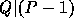 and an element
and an element 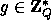 of order Q.
This task is achieved in three steps. First we find a prime Q of size
of order Q.
This task is achieved in three steps. First we find a prime Q of size
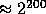 ,
then we find a prime P of size
,
then we find a prime P of size 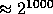 such that
such that
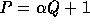 for some
for some
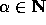 .
The density of primes in the natural numbers allows us to find appropriate
Q and
.
The density of primes in the natural numbers allows us to find appropriate
Q and  quite easily.
Finally we fix g to be
quite easily.
Finally we fix g to be 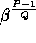 for some
for some 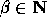 such that
such that 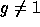 (the primality of Q ensures that the order of g is exactly
Q).
Note that we do not insist that P,Q and g be uniform in their range (since it
is not clear that such a requirement is essential for the Diffie-Hellman assumption).
(the primality of Q ensures that the order of g is exactly
Q).
Note that we do not insist that P,Q and g be uniform in their range (since it
is not clear that such a requirement is essential for the Diffie-Hellman assumption).
In order to implement f a large amount of random (or pseudo-random) keys are needed.
These keys can be generated by a pseudo-random generator which is a slight modification of
our construction f. Let 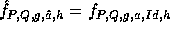 where
where 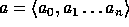 ,
, 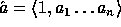 and
Id is the identity function. Following the proof in [3] it can be proven that
and
Id is the identity function. Following the proof in [3] it can be proven that 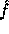 is pseudo-random on all inputs but 0. Using
is pseudo-random on all inputs but 0. Using 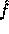 we implement the pseudo-random function :
we implement the pseudo-random function :
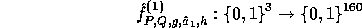
This implementation itself uses a seed of 2880 random bits : 800 for the random key 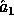 and 2080 for
the key y. Denoting
and 2080 for
the key y. Denoting 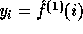 for
for 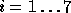 we have, by our above analysis, that each
we have, by our above analysis, that each 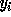 is pseudo-random in
is pseudo-random in 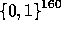 .
Thus
.
Thus 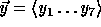 is pseudo-random in
is pseudo-random in 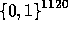 .
Using
.
Using 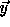 as a random source we can derive a new pseudo-random key,
as a random source we can derive a new pseudo-random key, 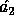 , with 5
elements by partitioning
, with 5
elements by partitioning 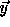 into chunks of length
into chunks of length 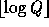 . Choosing Q such that
. Choosing Q such that 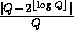 is negligible guarantees that the elements received remain pseudo-random in
is negligible guarantees that the elements received remain pseudo-random in 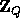 . Our new key now allows us to define
. Our new key now allows us to define
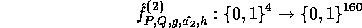
Repeating the above procedure grants us with a new pseudo-random 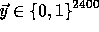 allowing
us to define
allowing
us to define
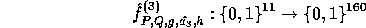
Using 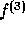 directly, all keys needed for our implementation can be manufactured.
directly, all keys needed for our implementation can be manufactured.
As mentioned, the above process uses a random seed of size 2880, this can be improved by replacing the
hash function h with a new hash function 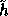 that has a smaller random key but still fulfills the
requirements regarding h stated in the previous section.
Therefore we define :
that has a smaller random key but still fulfills the
requirements regarding h stated in the previous section.
Therefore we define :
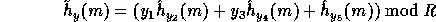
where 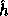 is the hash function defined in the previous section and
is the hash function defined in the previous section and 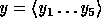 is a uniformly distributed sequence of elements in
is a uniformly distributed sequence of elements in 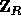 .
Note that for any pair of different inputs x,y the collision probability,
.
Note that for any pair of different inputs x,y the collision probability,
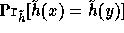 , is extremely close to
, is extremely close to 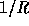 (at most
(at most 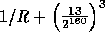 ) and the key of
) and the key of
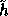 is of size 800 bits. This new hash function
is of size 800 bits. This new hash function 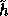 was not used originally in the
implementation of our pseudo-random function f because it is less efficient that h.
was not used originally in the
implementation of our pseudo-random function f because it is less efficient that h.
All in all the above construction with 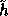 enables us to generate all random keys for the
implementation of f using a random seed of 1600 bits.
enables us to generate all random keys for the
implementation of f using a random seed of 1600 bits.
-
In order to compute 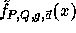 for |x| = n we need at most n multiplications modulo Q and one exponentiation modulo P.
for |x| = n we need at most n multiplications modulo Q and one exponentiation modulo P.
-
Computing the value of  for
for 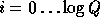 as preprocessing improves our efficiency by turning the single modular exponentiation into
as preprocessing improves our efficiency by turning the single modular exponentiation into 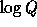 modular multiplications.
modular multiplications.
-
Additional preprocessing can improve the efficiency even further, for example computing the values of 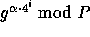 for all
for all 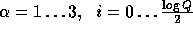 will turn the single modular exponentiation into
will turn the single modular exponentiation into 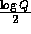 modular multiplications, and computing the values of
modular multiplications, and computing the values of
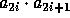 for
for 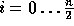 will turn the n modular multiplications into
will turn the n modular multiplications into 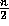 modular multiplications. For more details see [1].
modular multiplications. For more details see [1].
In our implementation we preprocessed by computing 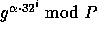 for all
for all 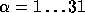 ,
,  . The reason
for this specific choice is that, for technical reasons, our
implementation performs part of its preprocessing on each run (and therefore there
was no point in a more extensive preprocessing). In general, the more preprocessing
done the faster the implementation will be.
. The reason
for this specific choice is that, for technical reasons, our
implementation performs part of its preprocessing on each run (and therefore there
was no point in a more extensive preprocessing). In general, the more preprocessing
done the faster the implementation will be.
-
The computation of f consists of two computations of 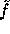 (that are not entirely independent) and two hash executions. All in all computing f with our constants takes about 0.5 seconds. As mentioned above, for technical reasons our implementation performs part of the preprocessing on each run, making our running time about one second per execution.
(that are not entirely independent) and two hash executions. All in all computing f with our constants takes about 0.5 seconds. As mentioned above, for technical reasons our implementation performs part of the preprocessing on each run, making our running time about one second per execution.
The construction we implemented is as secure as the decisional version of the
Diffie-Hellman [2] assumption.
For this to be true we need the keys to be random and secret.
In our implementation we used pseudo-random keys that are as secure as
the main construction (of f).
Regarding the secrecy of the keys, since we lack the means for secret-'bulletproof'
storage it might be feasible to access the keys.
References
- 1
-
E. F. Brickell, D. M. Gordon, K. S. McCurley and D. B. Wilson,
Fast exponentiation with precomputation,
Proc. Advances in Cryptology - EUROCRYPT '92,
LNCS, Springer, 1992, pp. 200--207.
- 2
-
W. Diffie and M. Hellman, New directions in cryptography,
IEEE Trans. Inform. Theory, vol. 22(6), 1976, pp. 644-654.
- 3
-
M. Naor and O. Reingold, Number-theoretic constructions of efficient pseudo-random functions. To appear in:
Proc. 38th IEEE Symp. on Foundations of Computer Science,
1997.
- 4
-
V. Shoup, NTL package, http://www.cs.wisc.edu/
 shoup/ntl.
shoup/ntl.
An Implementation of Efficient Pseudo-Random Functions
This document was generated using the LaTeX2HTML translator Version 95.1 (Fri Jan 20 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 pr.tex.
The translation was initiated by Langberg Michael on Tue Mar 31 16:55:04 IDT 1998
Langberg Michael
Tue Mar 31 16:55:04 IDT 1998
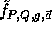 as follows:
The key of each pseudo-random function is a tuple,
as follows:
The key of each pseudo-random function is a tuple, 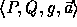 ,
where P is a large prime, Q a large prime divisor of P-1,
g an element of order Q in
,
where P is a large prime, Q a large prime divisor of P-1,
g an element of order Q in 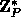 and
and 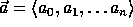 a uniformly distributed sequence of n+1 elements in
a uniformly distributed sequence of n+1 elements in 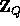 .
For any n-bit input,
.
For any n-bit input,
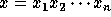 , the function
, the function 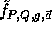 is defined by:
is defined by:
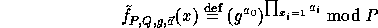
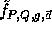 has domain
has domain 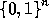 and range
and range
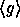 (the subgroup of
(the subgroup of 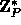 generated by g).
We now show how to adjust
generated by g).
We now show how to adjust 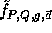 in order to get a
in order to get a 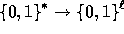 pseudo-random function.
I.e., the input of the function is a bit string of arbitrary
length and the output is a pseudo-random bit string of fixed length
pseudo-random function.
I.e., the input of the function is a bit string of arbitrary
length and the output is a pseudo-random bit string of fixed length 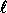 (instead of a pseudo-random element in
(instead of a pseudo-random element in 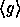 ).
For every input
).
For every input 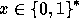 the function
the function
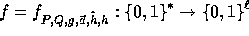 we implement is
defined by:
we implement is
defined by:
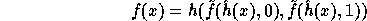
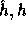 are two hash functions (defined below) and
are two hash functions (defined below) and 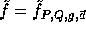 .
In words, the computation of f is as follows: First apply
.
In words, the computation of f is as follows: First apply 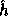 on the input
to get
on the input
to get 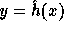 . Then compute two pseudo-random elements
. Then compute two pseudo-random elements 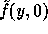 and
and 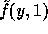 in
in 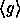 . Finally concatenate these elements
and hash the outcome by the second hash function h.
. Finally concatenate these elements
and hash the outcome by the second hash function h.
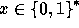 to
receive an element
to
receive an element 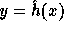 s.t.
s.t. 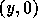 and
and 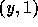 are in the domain of
the pseudo-random function
are in the domain of
the pseudo-random function 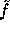 . In order for
. In order for 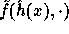 to be pseudo-random it is enough to require that for any two different inputs
to be pseudo-random it is enough to require that for any two different inputs
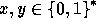 the probability of collision,
the probability of collision,
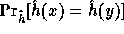 , is negligible.
To get this we define
, is negligible.
To get this we define 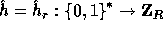 as follows:
as follows:
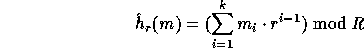
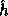 ) is a uniformly distributed
element in
) is a uniformly distributed
element in 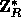 and the input m is partitioned into a sequence,
and the input m is partitioned into a sequence,
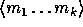 , of elements in
, of elements in 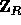 .
With this definition the collision probability on any two inputs of length at
most 160k is bounded by
.
With this definition the collision probability on any two inputs of length at
most 160k is bounded by 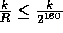 . The probability
of collision for some pair of inputs among
. The probability
of collision for some pair of inputs among 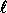 arbitrarily chosen inputs
is bounded by
arbitrarily chosen inputs
is bounded by 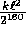 . For practical
values of
. For practical
values of 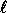 and k this probability is sufficiently small.
and k this probability is sufficiently small.
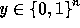 our core function
our core function 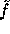 will
output a pseudo-random element in the subgroup
will
output a pseudo-random element in the subgroup 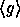 . Converting this
element into a pseudo-random value in
. Converting this
element into a pseudo-random value in 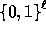 is done using a second hash
function
is done using a second hash
function 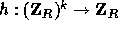 . The requirement from
h is that for any pair of different inputs x,y the collision probability
. The requirement from
h is that for any pair of different inputs x,y the collision probability
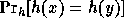 is
is 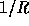 (or ``extremely close'' to this value).
Therefore, we cannot define
(or ``extremely close'' to this value).
Therefore, we cannot define 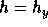 in the same way we defined
in the same way we defined 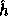 .
Rather than that we use the following definition:
.
Rather than that we use the following definition:
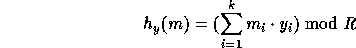
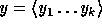 (the key of
(the key of 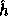 ) is a uniformly distributed sequence of elements in
) is a uniformly distributed sequence of elements in 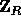 and the input
and the input 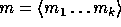 is a sequence
of elements in
is a sequence
of elements in 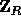 .
.
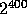 ,
then for all but a fraction
,
then for all but a fraction 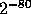 of the choices of y
the random variable
of the choices of y
the random variable 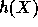 is of statistical distance at most
is of statistical distance at most 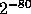 from the uniform distribution over
from the uniform distribution over 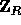 .
Therefore, if X is a pseudo-random element in such a set then (for all but
a fraction
.
Therefore, if X is a pseudo-random element in such a set then (for all but
a fraction 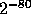 of the choices of y) the random variable
of the choices of y) the random variable 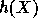 is a pseudo-random value in
is a pseudo-random value in 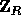 . Note that choosing R extremely close to
. Note that choosing R extremely close to 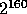 guarantees
guarantees 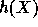 to be
pseudo-random in
to be
pseudo-random in 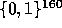 .
In our case, for any
.
In our case, for any 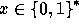 the value
the value 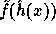 is pseudo-random
in
is pseudo-random
in 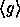 . Thus if we fix
. Thus if we fix 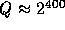 (implying the size of
(implying the size of 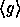 to be
to be 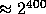 ) we can define our pseudo-random function as
) we can define our pseudo-random function as
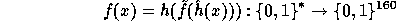
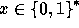 we compute the element
we compute the element
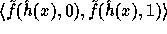 which is
pseudo-random in
which is
pseudo-random in 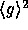 .
Since
.
Since 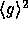 is of size approximately
is of size approximately 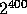 , we define
, we define
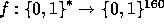 (by the previous analysis) to be
(by the previous analysis) to be
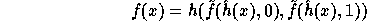
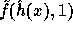 can be derived from the
exponent of g in the computation of
can be derived from the
exponent of g in the computation of 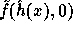 using a
single modular multiplication.
using a
single modular multiplication.
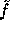 is a pseudo-random function.
As shown by Naor and Reingold, this is true as long as the decisional
version of the Diffie-Hellman assumption holds. In the current state of knowledge
it seems that choosing P of 1000 bits and Q of 200 bits makes this
assumption sufficiently safe.
is a pseudo-random function.
As shown by Naor and Reingold, this is true as long as the decisional
version of the Diffie-Hellman assumption holds. In the current state of knowledge
it seems that choosing P of 1000 bits and Q of 200 bits makes this
assumption sufficiently safe.
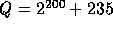 ,
, 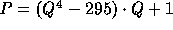 .
.
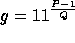 .
.
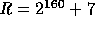 .
.
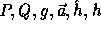 was generated
as follows:
was generated
as follows:
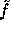 , we need two large primes P,Q s.t.
, we need two large primes P,Q s.t. 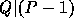 and an element
and an element 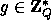 of order Q.
This task is achieved in three steps. First we find a prime Q of size
of order Q.
This task is achieved in three steps. First we find a prime Q of size
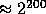 ,
then we find a prime P of size
,
then we find a prime P of size 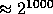 such that
such that
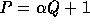 for some
for some
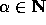 .
The density of primes in the natural numbers allows us to find appropriate
Q and
.
The density of primes in the natural numbers allows us to find appropriate
Q and  quite easily.
Finally we fix g to be
quite easily.
Finally we fix g to be 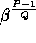 for some
for some 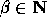 such that
such that 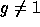 (the primality of Q ensures that the order of g is exactly
Q).
Note that we do not insist that P,Q and g be uniform in their range (since it
is not clear that such a requirement is essential for the Diffie-Hellman assumption).
(the primality of Q ensures that the order of g is exactly
Q).
Note that we do not insist that P,Q and g be uniform in their range (since it
is not clear that such a requirement is essential for the Diffie-Hellman assumption).
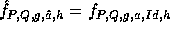 where
where 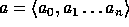 ,
, 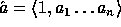 and
Id is the identity function. Following the proof in [
and
Id is the identity function. Following the proof in [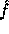 is pseudo-random on all inputs but 0. Using
is pseudo-random on all inputs but 0. Using 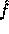 we implement the pseudo-random function :
we implement the pseudo-random function :
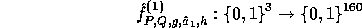
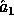 and 2080 for
the key y. Denoting
and 2080 for
the key y. Denoting 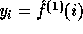 for
for 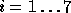 we have, by our above analysis, that each
we have, by our above analysis, that each 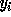 is pseudo-random in
is pseudo-random in 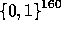 .
Thus
.
Thus 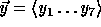 is pseudo-random in
is pseudo-random in 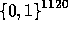 .
Using
.
Using 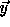 as a random source we can derive a new pseudo-random key,
as a random source we can derive a new pseudo-random key, 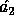 , with 5
elements by partitioning
, with 5
elements by partitioning 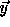 into chunks of length
into chunks of length 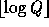 . Choosing Q such that
. Choosing Q such that 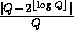 is negligible guarantees that the elements received remain pseudo-random in
is negligible guarantees that the elements received remain pseudo-random in 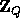 . Our new key now allows us to define
. Our new key now allows us to define
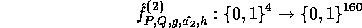
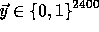 allowing
us to define
allowing
us to define
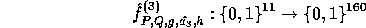
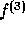 directly, all keys needed for our implementation can be manufactured.
directly, all keys needed for our implementation can be manufactured.
 that has a smaller random key but still fulfills the
requirements regarding h stated in the previous section.
Therefore we define :
that has a smaller random key but still fulfills the
requirements regarding h stated in the previous section.
Therefore we define :
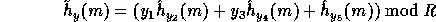
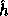 is the hash function defined in the previous section and
is the hash function defined in the previous section and 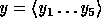 is a uniformly distributed sequence of elements in
is a uniformly distributed sequence of elements in 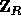 .
Note that for any pair of different inputs x,y the collision probability,
.
Note that for any pair of different inputs x,y the collision probability,
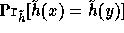 , is extremely close to
, is extremely close to 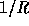 (at most
(at most 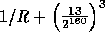 ) and the key of
) and the key of
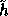 is of size 800 bits. This new hash function
is of size 800 bits. This new hash function 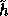 was not used originally in the
implementation of our pseudo-random function f because it is less efficient that h.
was not used originally in the
implementation of our pseudo-random function f because it is less efficient that h.
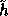 enables us to generate all random keys for the
implementation of f using a random seed of 1600 bits.
enables us to generate all random keys for the
implementation of f using a random seed of 1600 bits.
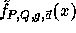 for |x| = n we need at most n multiplications modulo Q and one exponentiation modulo P.
for |x| = n we need at most n multiplications modulo Q and one exponentiation modulo P.
 for
for 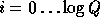 as preprocessing improves our efficiency by turning the single modular exponentiation into
as preprocessing improves our efficiency by turning the single modular exponentiation into 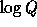 modular multiplications.
modular multiplications.
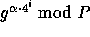 for all
for all 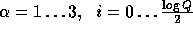 will turn the single modular exponentiation into
will turn the single modular exponentiation into 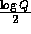 modular multiplications, and computing the values of
modular multiplications, and computing the values of
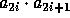 for
for 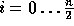 will turn the n modular multiplications into
will turn the n modular multiplications into 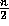 modular multiplications. For more details see [
modular multiplications. For more details see [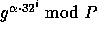 for all
for all 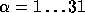 ,
,  . The reason
for this specific choice is that, for technical reasons, our
implementation performs part of its preprocessing on each run (and therefore there
was no point in a more extensive preprocessing). In general, the more preprocessing
done the faster the implementation will be.
. The reason
for this specific choice is that, for technical reasons, our
implementation performs part of its preprocessing on each run (and therefore there
was no point in a more extensive preprocessing). In general, the more preprocessing
done the faster the implementation will be.
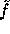 (that are not entirely independent) and two hash executions. All in all computing f with our constants takes about 0.5 seconds. As mentioned above, for technical reasons our implementation performs part of the preprocessing on each run, making our running time about one second per execution.
(that are not entirely independent) and two hash executions. All in all computing f with our constants takes about 0.5 seconds. As mentioned above, for technical reasons our implementation performs part of the preprocessing on each run, making our running time about one second per execution.
 shoup/ntl.
shoup/ntl.