Why limit cycles?

I have problems describing my field of interests. To put it simply, I love ordinary differential equations, especially the analytic theory of ODE’s. Unfortunately, today it sounds ambiguous and not fashionable. Yet I believe that the central position of this area, on the cross-roads of many paths, overweighs these considerations.

More specifically, what I am now interested in, is a number of problems spiritually related to the Hilbert 16^th problem, one of the two last problems from the Hilbert’s list of 1901, which still remain open (the other one is the Riemann Hypothesis on zeta-function). Hilbert asked, what can be the number and position of Poincare limit cycles, isolated closed (periodic) solutions of a polynomial differential equation on the plane of the form P(x,y)dx+Q(x,y)dy=0. Such question, if posed for very similar object, closed (compact) ovals of an algebraic curve H(x,y)=0, would be very natural (in fact, it is the first part of the same 16^th problem). The problem is that limit cycles almost never are algebraic curves, hence counting them is a completely different problem belonging to a totally different realm of transcendental analysis. Asking about transcendental objects a question appropriate for an algebraic context only, makes the problem transcendentally difficult beyond all considerations. The most advanced achievement towards its solution is the finiteness theorem (Yu. Ilyashenko, J. Ecalle, 1991-1992) claiming that the number in question is finite (in other words, that the question is well-formed!). Even this statement requires a book-long proof.

On a more basic level, the same phenomenon manifests itself in the following way. Polynomial and more generally algebraic functions of one complex variable, and their rational combinations, always admit upper bounds for the number of their isolated zeros. The only operation that destroys algebraicity, is solving differential equations (in particular, integration and exponentiation). Solutions of polynomial differential equations may exhibit totally different properties (compare real non-integer powers of a complex argument which inherit many properties of usual monomials and the sine/cosine functions that have infinitely many zeros). Analyzing reasons for such (mis)behavior requires tools from so distant areas as integral geometry, singularity theory and commutative algebra.

One particular form of the “algebraic-like” question about transcendental objects is known as the tangential or infinitesimal Hilbert problem. Consider an infinite collection of real level curves H(x,y)=z, where z ranges over all real values, and along each level curve integrate a polynomial differential 1-form P(x,y)dx+Q(x,y)dy. The result is a (multivalued) function of the argument z, called Abelian integral. The problem is to find the number of “roots” of this function, i.e., the number of algebraic ovals yielding zero values for this integral. Despite its seemingly elementary character, the problem is also open to a very large extent. For instance, only in March 2002 it was proved that the number of such “roots” (ovals) can be at most 2 if all polynomials H,P,Q are quadratic.

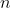In August 2008, together with Gal Binyamini and Dmitry Novikov, we finally succeeded in solving this problem explicitly and proved that the number of isolated zeros of an Abelian integral does not exceed , where is the maximum of the degrees of 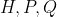and is an explicit polynomial of degree not exceeding, say, 60. This result on one hand settles a 50+ years-old problem, on the other hand, leads to a number of new intriguing questions.

These and adjacent issues are explained in details in several lecture notes and survey papers that I wrote on this subject. For more information you are invited to browse the complete list of (online) papers available on this site.

Yakovenko, S. Quantitative theory of ordinary differential equations and tangential Hilbert 16^th problem, Preprint math.DS/0104140 (2001), 1--69, Lecture notes of the course delivered on the Workshop "Asymptotic series, differential algebra and finiteness theorems" (Montreal, 2000), to appear in CRM Proceedings.

Yakovenko, S. On functions and curves defined by ordinary differential equations. The Arnoldfest (Toronto, ON, 1997),  Fields Inst. Communications, 24 (1999), 497--525, Amer. Math. Soc., Providence, RI, 1999

Research report (1996) mentions and briefly surveys some of the previous work

Ilyashenko, Yu., Yakovenko, S. Concerning the Hilbert sixteenth problem. Concerning the Hilbert 16th problem, 1--19, Amer. Math. Soc. Transl. Ser. 2, 165, Amer. Math. Soc., Providence, RI, 1995

I hope to put here a list of problems that I for some reasons believe to be important, interesting or promising.